Theory:
Construction of the Nine-Point Circle
1. Draw a triangle ABC.
2. Construct the midpoints of the three sides. Label them as L, M, N.
3. Construct the feet of the altitudes of the triangle ABC. Label them as D, E, F. Label the point of intersection of the three altitudes as H. This is also called the orthocenter.
4. Construct the midpoints of the segments AH, BH, CH. Label them as X, Y, Z.
First, notice the nine points, L,M,N,D,E,F,X,Y, Z, lie in a circle.
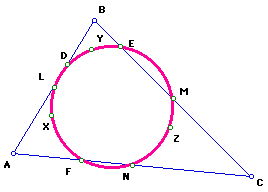
This circle is called the Nine-Point Circle.
To find the center of the Nine-Point Circle, construct the circumscribed circle for triangle LMN. Label the center as U.
The center of the circumscribed circle for triangle LMN will also be the center of the Nine-Point Circle labeled as U.
A second way to find the Nine-Point Center is to begin by constructing the circumcircle for triangle ABC. Label the circumcenter as CC.
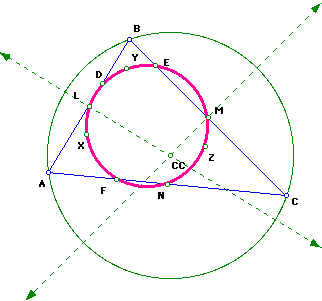
The center of the Nine-Point Circle, U, is the midpoint from the orthocenter, H, and the circumcenter, CC, of triangle ABC.
Theory and image uoted from this link
Finding the center of a circumcircle of a triangle.
1)mid point of the sides
2)slope of the sides
3)slope of perpendicular bisectors of the sides
4)eqn of the bisectors
5)solve the eqn and find the circumcenter.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
#include <iostream> #include <math.h> #include <stdio.h> #define slop 10000000000 using namespace std; int main() { double x1, y1, x2, y2, x3, y3; double a,b,c,s; double r,Gx,Gy; double Lx,Ly,Mx,My,Nx,Ny; double LMx,LMy,MNx,MNy,NLx,NLy; double slope_M_NL,slope_N_LM,slope_L_MN; double x,y; while(cin>>x1) { cin>>y1>>x2>>y2>>x3>>y3; if(x1==-1 && x2==-1 && x3==-1 && y1==-1 && y2==-1 && y3==-1) break; slope_M_NL=slop; slope_N_LM=slop; slope_L_MN=slop; a=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); b=sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2)); c=sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3)); s=(a+b+c)/2; // radius of the circumcircle of triangle // R= abc/(4*root(s*(s-a)*(s-b)*(s-c))); //radius of nine point circle of that triangle r=R/2; r = (a*b*c)/(8*sqrt(s*(s-a)*(s-b)*(s-c))); Lx= (x1+x2)/2; Ly= (y1+y2)/2; Mx= (x2+x3)/2; My= (y2+y3)/2; Nx= (x1+x3)/2; Ny= (y1+y3)/2; //finding circumcenter of the triangle LMN /*Steps: 1)mid point of the sides 2)slope of the sides 3)slope of perpendicular bisectors of the sides 4)eqn of the bisectors 5)solve the eqn and find the circumcenter. */ LMx=(Lx+Mx)/2; LMy=(Ly+My)/2; MNx=(Mx+Nx)/2; MNy=(My+Ny)/2; NLx=(Nx+Lx)/2; NLy=(Ny+Ly)/2; if((Ly-My)!=0) { slope_N_LM=(-1)*((Lx-Mx)/(Ly-My)); } if((Ny-My)!=0) { slope_L_MN=(-1)*((Nx-Mx)/(Ny-My)); } if((Ny-Ly)) { slope_M_NL=(-1)*((Nx-Lx)/(Ny-Ly)); } //finding c of the bisectors double C_M_NL=slop; double C_L_MN=slop; double C_N_LM=slop; if(slope_M_NL!=slop) { C_M_NL=NLy-slope_M_NL*NLx; } if(slope_L_MN!=slop) { C_L_MN=MNy-slope_L_MN*MNx; if(C_M_NL!=slop) { x=(C_M_NL-C_L_MN)/(slope_L_MN-slope_M_NL); y=x*slope_L_MN+C_L_MN; printf("%.6lf %.6lf %.6lf\n",x,y,r); continue; } } if(slope_N_LM!=slop) { C_N_LM=LMy-slope_N_LM*LMx; if(C_L_MN!=slop) { x=(C_L_MN-C_N_LM)/(slope_N_LM-slope_L_MN); y=x*slope_N_LM+C_N_LM; printf("%.6lf %.6lf %.6lf\n",x,y,r); } else { x=(C_M_NL-C_N_LM)/(slope_N_LM-slope_M_NL); y=x*slope_N_LM+C_N_LM; printf("%.6lf %.6lf %.6lf\n",x,y,r); } } // Gx= (Lx+Mx+Nx)/3; // Gy= (Ly+My+Ny)/3; // printf("%.6lf %.6lf %.6lf\n",Gx,Gy,r); } return 0; } |